過日、小学五年生の孫が算数の教科書を持ってやってきました。母親から爺さんに勉強を教えてもらいなさいと言われたのだそうです。
家内かから聞いていたのですが、数学が苦手なので教えてやってもらえないかと頼まれたのだそうです。彼はぼくがもう使わなくなったPowerBookでゲームをするのが楽しみで暇があれがやってくるのが常なのです。そうした時に、折に触れて日本の神話の話やダーウィンの進化論と白人の植民地支配などの話をしてやると、どれだけ理解しているのはわからないのですが、意外と熱心に聞き入ったりするのです。

吉田光由が著した塵劫記。
江戸初期に日本中で読まれた。

ぼくたちが知らない「京」以上の数も書いてある。
そのひとつが俵の問題です。「図のように俵が積み上げられている。一番下が13俵の時、全部では何俵か。」
下に示したのは、その解で、普通なら1、2、3と足してゆき13まで足すと答えがでる。しかしここでは次のような解が示されている。下図に示されているのは、俵の山を逆さまにして並べ、1段目の13+1に段数の13を掛け合わせて2で割るというやりかたです。

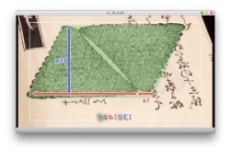
とまあ、こんな具合に話をしてから、教科書を開きました。今習っている辺りをきいてから、その少し前に戻ると、合同の概念が説明されていたので、どういうことかと聞くと「きっちり重ね合わせられること」という答えです。「そうやなあ。その通り」
数ページ先に長方形、平行四辺形、台形の三つが並んで書いてあるページがあります。
そこで、ぼくはこの三つの図形の同じところ違っているところはどこかを考えようと持ちかけました。
「長方形と平行四辺形はどう違う?」
「ひしゃげてる」「うん。たしかに。でももっと細かにどこがどうかを考えてみよう」
こうした場合にぼくのやり方は、答えを急かしません。気長に気長に答えを待つ主義です。時間は問題ではない。色々な思考の錯誤の過程が重要だと思うからです。
少し時間がかかって、対する辺が平行であることに気がつきました。
「たしかに。では違っているところはどこなんや」
どうしてかは分からないのですが、ここからが結構大変で一方に直角があることに気づくまでにだいぶ時間がかかりました。「そうやなあ。長方形には直角があるけれど平行四辺形には一つもないなあ」
「では次は、平行四辺形と台形で同じことを考えてみよう」
これもなかなか答えが出ませんでした。ようやく平行である辺が2組と1組であることに気づきました。
「そういうことみたいや。では三つの図形を一緒にして同じところ違っているところをまとめて言ってみて」
同じところは四辺形であること。違うところは直角の有無。平行辺の数であることが結論づけられました。
台形には平行辺があるからひっくり返して並べると平行四辺形になり、容積計算ができることが理解できたようでした。こんなことは、ぼくも考えたのは初めてで、結構楽しい時間でした。
「あんなあ。答えが得られないと言って諦めたらあかん。考え続けたらきっと答えは得られるもんなんや。そう信じなあかん」とぼくは教えたのです。
この約2時間ほどで孫は結構疲れたようだったので終わることにしました。帰り際に宿題として、『塵劫記』に載っている問題を出すことにしました。
紙に三つの枡の絵を描いて、
<10升(1斗)升にいっぱいの水が張ってある。他に7升と3升の枡がある。この三つを使って水を5升と5升に分けなさい>
「枡ってなに?」と聞くので、容器ということと説明し、升というのはべつにリットルと考えてもいいといい、何日かかってもいいから考えるんやぞと付け加えたのです。
皆さんもお考えになってはいかがでしょうか。
